 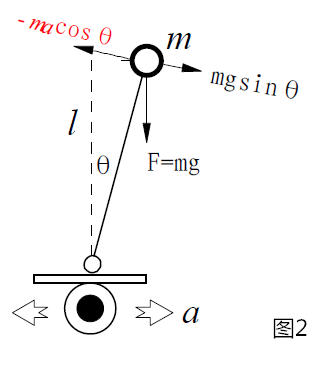
控制平衡小车,使得它作加速运动。这样站在小车上(非惯性系,以车轮作为坐标原点)分析倒立摆受力,它就会受到额外的惯性力,该力与车轮的加速度方向相反,大小成正比。这样倒立摆(如图2)所受到的回复力为:公式1 F = mg sin θ-ma cos θ≈mg θ-mk1θ 式1中,由于θ很小,所以进行了线性化。假设负反馈控制是车轮加速度a与偏角θ成正比,比例为k1。如果比例k1>g,(g是重力加速度)那么回复力的方向便于位移方向相反了。 而为了让倒立摆能够尽快回到垂直位置稳定下来,还需要增加阻尼力。增加的阻尼力与偏角的速度成正比,方向相反,因此公式1可改为: F = mg θ-mk1 θ -mk2 θ` 按照上述倒立摆的模型,可得出控制小车车轮加速度的算法: a =k1θ+k2θ` 式中θ为小车角度,θ`为角速度。k1 k2都是比例系数 根据上述内容,建立速度的比例微分负反馈控制,根据基本控制理论讨论小车通过闭环控制保持稳定的条件(这里需要对控制理论有基本了解)。假设外力干扰引起车模产生角加速度x(t)。沿着垂直于车模地盘方向进行受力分析,可以得到车模倾角与车轮运动加速度以及外力干扰加速度a(t)x(t)之间的运动方程。如图3所示。 在角度反馈控制中,与角度成比例的控制量是称为比例控制;与角速度成比例的控制量称为微分控制(角速度是角度的微分)。因此上面系数k1,k2分别称为比例和微分控制参数。其中微分参数相当于阻尼力,可以有效抑制车模震荡。通过微分抑制控制震荡的思想在后面的速度和方向控制中也同样适用。 总结控制车模直立稳定的条件如下: (1)能够精确测量车模倾角θ的大小和角速度θ'的大小; (2)可以控制车轮的加速度。 上述控制实际结果是小车与地面不是严格垂直,而是存在一个对应的倾角。在重力的作用下,小车会朝着一个方面加速前进。为了保持小车的静止或者匀速运动需要消除这个安装误差。在实际小车制作过程中需要进行机械调整和软件参数设置。另外需要通过软件中的速度控制来实现速度的稳定性。在小车角度控制中出现的小车倾角偏差,使得小车在倾斜的方向上产生加速。这个结果可以用来进行小车的速度控制。下面将利用这个原理来调节小车的速度。
|