项目介绍:
本项目是一个可以复原三阶魔方的机器。Cube Robot -> Cubot. 目前需要人手工把各个面色块的颜色输入电脑,通过一个C++程序求出解法,然后将解法复制到Arduino的代码中再上传,Arduino随后通过驱动器控制步进电机执行解法。
视频地址:https://m.weibo.cn/status/4169240011431230
代码地址: https://github.com/g20150120/cubot
涉及的元器件:
6* 42两相四线步进电机 (额定电压3.3V 额定电流1.5A)
6* L298N驱动板
6* 自行设计、3D打印的连接件,使步进电机可以直接转动魔方的中心块,同时容易脱开。
1* 直流稳压电源 (0-15V可调 最大2A)
1* Arduino MEGA2560 (总共需要 4*6=24 个digital output来控制驱动和步进电机,UNO无法胜任)
面包板两块、杜邦线若干
我在高一下学期,大约是2016年4/5月份萌发了制作魔方机器人的想法。高中参与了一些计算机科学、电子工程方面的课程,同时又加入了魔方社,而且我从小又对机械模型有浓厚的兴趣,如此机缘巧合之下,我产生了这个想法。整件事情谈何容易,起初我有的只是一个Arduino UNO,一个GAN 356, 不过还有无限的热情和不轻易放弃的执着。
我首先有了一个大概的思路。有别于网上已有的魔方机器人的设计细节,我决定通过3D打印的连接件嵌入魔方中心块内部的缺口,直接与电机相连;外部是一个支架,把魔方和六个面的电机架空。程序分为两部分,第一部分由电脑执行,输入魔方6个面上总计6* 3*3=54个色块的颜色,输出解法;第二部分由Arduino执行,输入解法,控制电机完成旋转。电机方面只有步进电机能不断旋转出指定的角度,考虑性能和价格后我选择了工业级的42号步进电机,额定3.3V 1.5A。又由于单片机输出的高低电平并不能直接控制步进电机,我比较后选择了经典的L298N驱动芯片。确定这些以后我简单计算了一下电气参数,发现现有的Arduino UNO的数字信号输出端口数量不够;另一方面,通过电脑给Arduino供电,再给驱动芯片和步进电机供电的电路因为USB接口和Arduino内部的限流设计,事实上无法工作。考虑到这些问题,我选择了功能更强大的Arduino MEGA2560,又购买了一个0-15V连续可调电压,最大电流2A的直流稳压电源。
初步的设计完成以后我决定先完成所有的代码。有别于人类复原魔方使用的层先法和CFOP方法,计算机求解魔方普遍使用的Thistlethwaite Method以数学中的群论作为理论依据,把打乱的魔方视为魔方群中的一个群元素,逐步降解魔方所处的群到更小的子群,最后到单位子群,即还原状态。这个算法有多种编程语言的多个实现方式,我试图寻找并调试出高效易懂的实现代码。给这个算法输入的魔方状态不再是用各个小色块表示,而是确定了整个魔方的朝向以后直接用棱块和角块的相对位置关系和朝向表示 (形如 UF UR UB UL DF DR DB DL FR FL BR BL UFR URB UBL ULF DRF DFL DLB DBR)。 这也给我提出了一个新的要求:编写一个程序把用颜色展开图形式表示的魔方转换成如上,用一个棱块和角块的字符串表示的魔方。我自己体验了几次把打乱的魔方转换成该字符串的过程,找到了对应规律,归纳出了对应方法,存入几个常量数组,通过对这些数组的巧妙访问高效地使独立的六个面形成一个完整的二维数组表示的展开图,并且转化为最终的字符串;后续的修改还使得各个面输入时只要方向正确,不必按照特定的顺序,带来了一定的方便;不足之处是这个代码不能检查出是否有颜色输错、该魔方是否可以通过正常的转动形成。
[mw_shl_code=cpp,true]char cube[9][12];
/*
cube[x][y] 储存9行12列的颜色展开图
XXX
XWX
XXX
XXX XXX XXX XXX
XOX XGX XRX XBX
XXX XXX XXX XXX
XXX
XYX
XXX
*/
const int
//展开图中六个面填色的起始位置 0-5为 GWORYB
start_x[6]={3,0,3,3,6,3},
start_y[6]={3,3,0,6,3,9},
//代表颜色信息和位置信息的关系 人工总结
edge_x[24]={2,3,1,3,0,3 ,1,3,6,5,7,5,8,5 ,7,5,4,4,4,4,4,4,4 ,4},
edge_y[24]={4,4,5,7,4,10,3,1,4,4,5,7,4,10,3,1,5,6,3,2,9,8,11,0},
apex_x[24]={2,3,3,0,3,3,0,3 ,3,2,3,3,6,5,5,6,5,5,8,5,5 ,8,5,5},
apex_y[24]={5,5,6,5,8,9,3,11,0,3,2,3,5,6,5,3,3,2,3,0,11,5,9,8};
int func(char ch)
{
//对应start_x/start_y中的颜色顺序
if(ch=='W')
return 1;
if(ch=='G')
return 0;
if(ch=='O')
return 2;
if(ch=='R')
return 3;
if(ch=='B')
return 5;
if(ch=='Y')
return 4;
return 0;
}
char convert(char ch)
{
//将展开图中的颜色信息转换为FU LR etc的位置信息
//其中 绿色为F 白色为U 形如 cube[9][12]
if(ch=='W')
return 'U';
if(ch=='G')
return 'F';
if(ch=='O')
return 'L';
if(ch=='R')
return 'R';
if(ch=='B')
return 'B';
if(ch=='Y')
return 'D';
return 0;
}
int main()
{
//do sth.
//储存一个面的3*3矩阵
string tmp[3];
for(int ii=0;ii<6;ii++)//执行六次 读取六个面的3*3矩阵
{
for(int jj=0;jj<3;jj++)//读取一个矩阵的三行
cin>>tmp[jj];
//tmp[1][1]记录中心块颜色 从而确定这一面的颜色 和 在展开图中的相对位置
int q=func(tmp[1][1]);
//将tmp中的信息转存到cube[9][12]展开图中
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
cube[start_x[q]+i][start_y[q]+j]=tmp[j];
}
//argv[1-20]存储魔方的状态 值为 UF DBR etc
string argv[21];
//后面通过+=写入数据 务必先初始化置为空
for(int i=0;i<21;i++)
argv="";
//代表现在向argv[index]写入数据
int index=1;
for(int i=0;i<24;i++)
{
//把颜色信息转换成位置信息
argv[index]+=convert(cube[edge_x][edge_y]);
//前12组表示棱的位置 每组两个 UF UR etc
if(i%2==1)
index++;
}
for(int i=0;i<24;i++)
{
//把颜色信息转换成位置信息
argv[index]+=convert(cube[apex_x][apex_y]);
//后8组表示角的位置 每组三个 ULF DBR etc
if(i%3==2 && i!=23)
index++;
}
//do sth.
return 0;
}
[/mw_shl_code]
上面是我进行魔方表示方法转换的代码。求解魔方的代码涉及群论知识,超出了我的知识水平,感兴趣的可以查阅我的GitHub里面的 SOLVECUBE.cpp 了解具体的实现方法。表示魔方状态的核心数据结构是一个 vector<int> ,求解核心算法是BFS。
计算机求解部分做的差不多了以后我就开始写Arduino的代码。这个代码需要阅读解法,并控制对应的步进电机旋转对应的方向和度数。首先,所有的参数(电机速度、步数、步进角、延迟时间、顺逆时针旋转等等)都预先用常变量定义在代码最开始;定义一个字符串保存之前的程序算得的解法,两个一读遍历字符串,得到哪一面旋转多少次,接着通过switch语句嵌套和Stepper.h的函数具体控制哪个电机旋转多少步。起初的代码并不简洁美观,直到我之后重构代码引入了一个常量数组代替了第二层switch语句。
[mw_shl_code=cpp,true]#include <Stepper.h>
#include <String.h>
using namespace std;
//R1L3F2B2R1L3U1L1R3B2F2L1R3=D
/*
All the parameters below are well-adjusted. Please don't change anything except time.
*/
const int STEPS = 205; // 360/1.8
const int stepperSpeed = 240; // rpm 15.8V
const int timeBetweenMoves = 5; // ms between U2 R2 or U R etc.
const int timeBetweenComs = 1000*8; // ms between commands
const int steps_90 = 3*STEPS/4 ;
const int steps_180 = STEPS/2;
const int steps_270 = STEPS/4;
const int _angle[4]={0,steps_90,steps_180,steps_270};
// U2 -> stepperU.step(_angle[2]);
String command = "";
// adjust them according to your wiring
Stepper FF(STEPS,28,29,30,31);
Stepper DD(STEPS,22,23,24,25);
Stepper BB(STEPS,34,35,36,37);
/**/
Stepper LL(STEPS,38,39,40,41);
Stepper UU(STEPS,44,45,46,47);
Stepper RR(STEPS,50,51,52,53);
void Getcom();
void Solve();
void setup()
{
FF.setSpeed(stepperSpeed);
UU.setSpeed(stepperSpeed);
RR.setSpeed(stepperSpeed);
/**/
LL.setSpeed(stepperSpeed);
DD.setSpeed(stepperSpeed);
BB.setSpeed(stepperSpeed);
pinMode(13,OUTPUT);
}
void loop()
{
delay(timeBetweenComs);
command = "";
Getcom();
}
// I was going to implement a funtion to receive solutions from serial monitor but did not manage to do so.
// I just simply paste the solution here and upload the code.
void Getcom()
{
command = "U2F2L2D2B2U2F2L2F2R2F2U1L2R2F2U3B2U1L2U3R1U3D2F2R1D2U1F1U1B1R3L2U3";
Solve();
}
void Solve()
{
int com_len=command.length();
for(int i=0;i<com_len;i+=2)
{
char ch=command;
int n=command[i+1]-'0';
//FULRDB
switch(ch)
{
case 'F':FF.step(_angle[n]); for(int i=FF.motor_pin_1;i<FF.motor_pin_1+4;i++) digitalWrite(i,LOW); break;
case 'U':UU.step(_angle[n]); for(int i=UU.motor_pin_1;i<UU.motor_pin_1+4;i++) digitalWrite(i,LOW); break;
case 'L'  L.step(_angle[n]); for(int i=LL.motor_pin_1;i<LL.motor_pin_1+4;i++) digitalWrite(i,LOW); break;
case 'R':RR.step(_angle[n]); for(int i=RR.motor_pin_1;i<RR.motor_pin_1+4;i++) digitalWrite(i,LOW); break;
case 'D'  D.step(_angle[n]); for(int i=DD.motor_pin_1;i<DD.motor_pin_1+4;i++) digitalWrite(i,LOW); break;
case 'B':BB.step(_angle[n]); for(int i=BB.motor_pin_1;i<BB.motor_pin_1+4;i++) digitalWrite(i,LOW); break;
}
// Turning off the digital output of every pin after steps are made is crutial; otherwise, the current will be too large.
// To do so, motor_pin_i in Stepper.h must be removed from private to public.
digitalWrite(13,HIGH);
delay(timeBetweenMoves);
digitalWrite(13,LOW);
// These scope is to determine whether the chip is executing the solution.
}
}[/mw_shl_code]
上面的代码是我具体的实现。

接下来最关键的就是接线了。具体接线其实并无对错之分,只需使得步进电机的时序图和Stepper.h中的控制函数通过接线对应好即可。
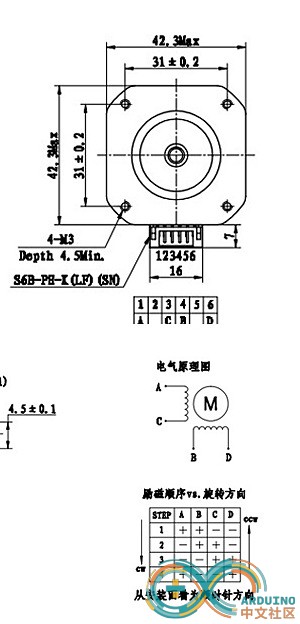
(按照一些习惯,这里的A B C D也表示成A+ A- B+ B-)
[mw_shl_code=cpp,true]/*
* The sequence of control signals for 4 control wires is as follows:
*
* Step C0 C1 C2 C3
* 1 1 0 1 0
* 2 0 1 1 0
* 3 0 1 0 1
* 4 1 0 0 1
*/[/mw_shl_code]
阅读Stepper.h中的注释,得知头文件中的函数将要输出的逻辑信号。
于是,我把连续四个digital output接入驱动板的IN 1234,驱动版的OUT 1234和电机的A+ A- B+ B-连接好。声明电机时使用 [mw_shl_code=cpp,true]Stepper FF(STEPS,28,29,30,31);[/mw_shl_code] 即可。为了防止电流超出电源的限流措施,也为了增强旋转过程中的容错能力、防止卡死,每个电机在不需要旋转时必须终止给它的所有digital output,即 [mw_shl_code=cpp,true]for(int i=FF.motor_pin_1;i<FF.motor_pin_1+4;i++) digitalWrite(i,LOW);[/mw_shl_code] 因此,Stepper.h 需要修改,把 motor_pin_1 从private移到public即可。电源方面,驱动板上所有的+12V连接电源的正极;所有GND和Arduino的GND连在一起,连接电源的负极。Arduino通过USB串口由电脑供电。
接下来的工作就是实现魔方中心块和步进电机的连接。我希望设计出简单、可靠、易脱开的连接机制,方便即时的连接、脱开。我想到了可换头的螺丝刀,拧螺丝的头末端是一个正六边形,插入一个略大于此六边形的孔洞中用磁铁吸住。虽然可以随时插拔,但是在旋转过程中不会滑动,而是紧紧锁住。我设想用一个空心的八棱柱卡在魔方中心块内截面为圆角矩形的孔洞中,另一端是一个六棱柱的孔洞;连接件的另一半,一端是一个略小的六棱柱,插入孔洞中带动魔方旋转,另一端的凹槽与步进电机的轴卡住。以这个想法为支撑,我记下了步进电机图纸中的各个尺寸,再用游标卡尺测得魔方中所需的宽度、深度等数值,用尺规画出了二维设计图;随后使用CAD将此画成机械零件设计图,其中包括主视图的剖面图;然后交由淘宝网店3D建模;再发给3D打印店打印出最终的成品。
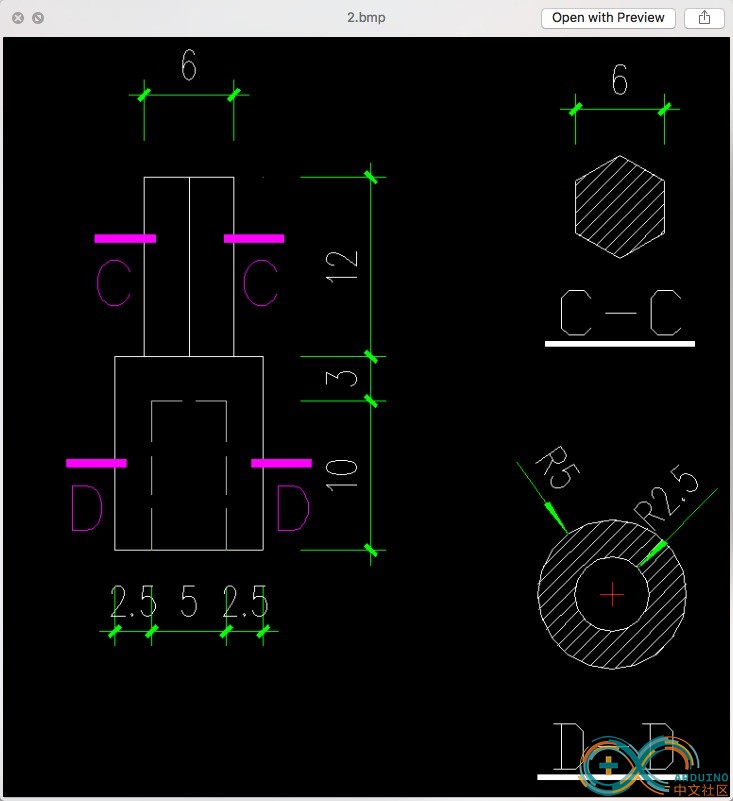
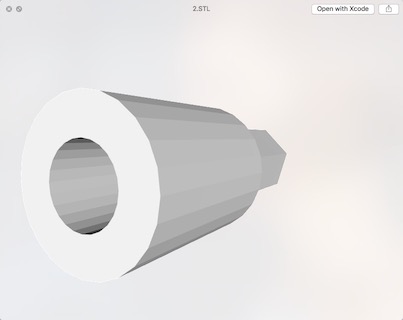
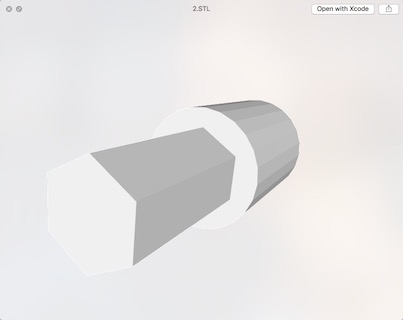
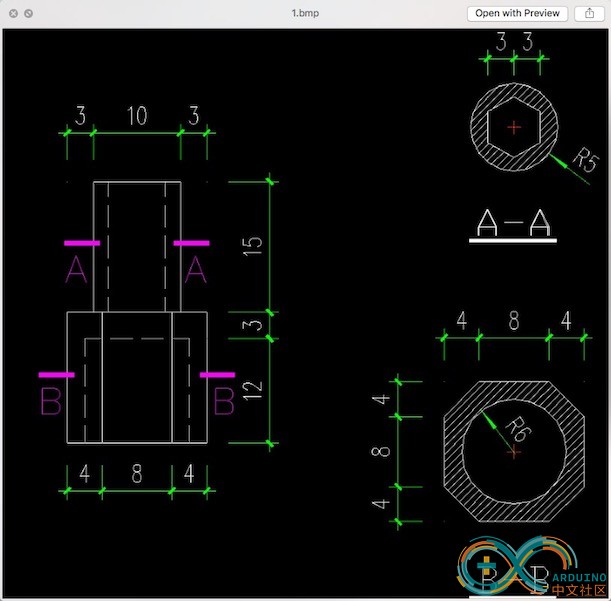

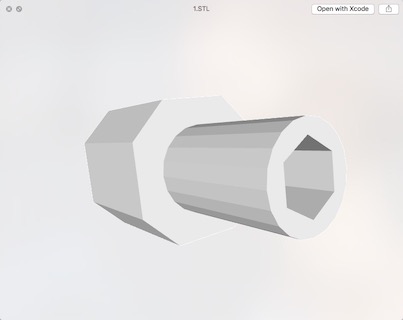
这个连接件可以使得电机直接带动魔方每一面旋转,同时也很容易将二者脱开。参考了可以换头的磁性螺丝刀的设计。
最终,我把机器组装起来,代码编译好备用。历经了一阵辛苦的调参,包括调整步进角尽可能抵消旋转误差;调整一个合适的旋转速度,减少失步,同时兼顾速度,电流又不能超出限制;调一个合适的间隔时间,每次旋转之间不要间隔太久;最后就是一些细节,逆时针顺时针实现、校正等等。上面的视频中可以看到,整个魔方机器人运行良好。
未来希望给这个魔方机器人做一个稳定的支架,以及添加自动识别魔方颜色的功能。
解魔方的算法叫 Thistlethwaite Method ,根据群论的思想求解魔方。我找到了很多相关资料,还包括一些以后准备做的OpenCV魔方颜色识别。遗憾的是,目前水平有限,没能理解、运用。如果有感兴趣,之后可以共享这些资料。只想了解大概的话,http://tieba.baidu.com/p/1738194036 等等讲的很不错。如果有群论和OpenCV大神,请指导一下!
具体的代码操作流程和一些关键的注释写在了GitHub。
|
