|
|
本帖最后由 t3486784401 于 2020-4-18 03:21 编辑
首先感谢 M5Stack 团队这次给试用 TCS3472 颜色识别模块!
在接下来的日子中我会逐步发表测评帖子,记录项目“色控电子琴”的开发历程。
本帖是第 1 篇测评,内容为发现了 M5Stack 官方文档的一处错误。
--------------------------------------------------------------------
【背景】
收到 TCS3472 以后,被 M5Stack 官方做事的细致程度震惊到了,完全是产品级的模块。
运行 Adafruit 的标准库以后,获得了 R/G/B 原始的数据,顺手换算了一下 CIE-1931 色度。
结果一换算不打紧,直接出现了负数坐标,完全跟传说的马蹄区域不搭边。
下图是申请 TCS3472 过程的介绍帖,在 M5Stack 官网的文档中也提及了这个换算公式。
官方文档地址:https://docs.m5stack.com/#/zh_CN/unit/color

按照换算公式,知道 R/G/B 以后可以算得 X/Y,并对应到色度图坐标中。
然而实际按照介绍的系数,会算出负数 X/Y,完全摸不着头脑。
典型例子:(r,g,b)= (82,41,56);计算得 (xc,yc)= (-0.68,-1.13)
【分析】
我第一反应是有计算溢出了,但是查了代码都没有任何进展。
甚至在 Adafruit 的 TCS3472 库中,都找到了相同系数的计算代码(但作者写明了 Y 是亮度):

然而这并不能打消疑虑,索性去查了 CIE 的各种颜色空间。
查阅资料,发现 CIE1931 包括若干个颜色空间(注意大小写有区别):
CIE-RGB:常见的R/G/B分量,TCS3472输出可认为属于该空间;
CIE-XYZ:即 CIE-1931,马蹄色度图位于该空间 XOY 平面;
CIE-xyY:前两维度 xy 同 CIE-XYZ,第三维度 Y 为亮度,算法系数出现在了:
①Adafruit 的代码中,②M5Stack 官方文档的色度图 y 坐标计算中
显然 M5Stack 误将 CIE-xyY 的 Y(亮度)算法当成了 CIE-XYZ 的纵坐标 Y,
导致 RGB 换算后超出马蹄图坐标。
【验证】
为了彻底搞清楚 M5Stack 官方文档上给的换算矩阵到底什么样,将其算法计为 Run1(附件有M代码);
对照网上下载了 CIE-XYZ 颜色空间的换算代码(下图),该算法计为 Run2(附件有M代码),
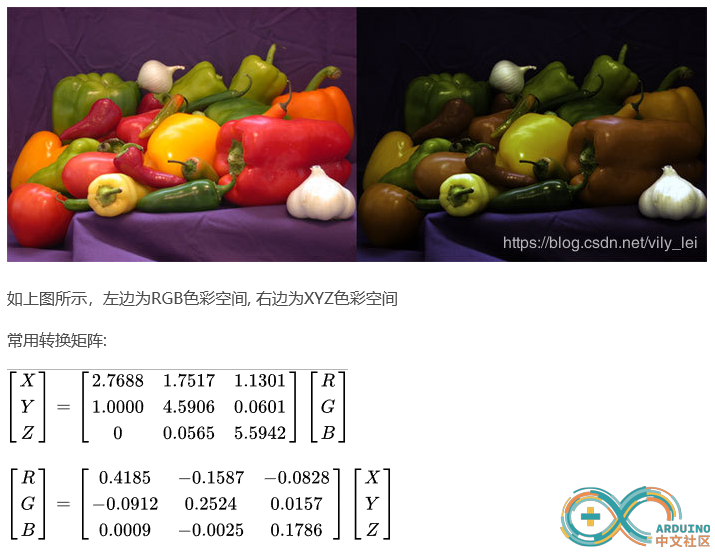
分别使用 MATLAB 将 R/G/B= 0:20 这样 21*21*21 细分的 CIE-RGB 颜色空间映射成 x,y 坐标,
Run1(Adafruit源码, M5Stack文档):
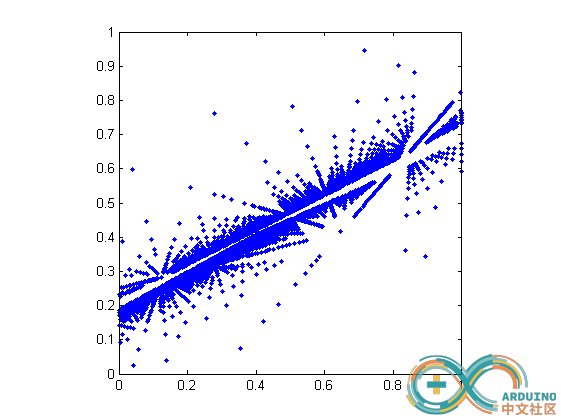
Run2(下载的 RGB 转 XYZ 矩阵):
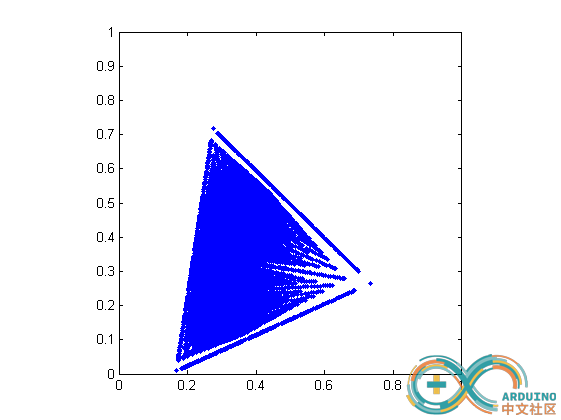
显然 Run2 矩阵的结果都落在了马蹄图的区域内,这才是正确的 CIE-RGB 转 CIE-XYZ 矩阵。
附上另一张与马蹄图叠加的结果,虽然我这个 21*21*21 的分辨率不够细腻,但足以说明问题。
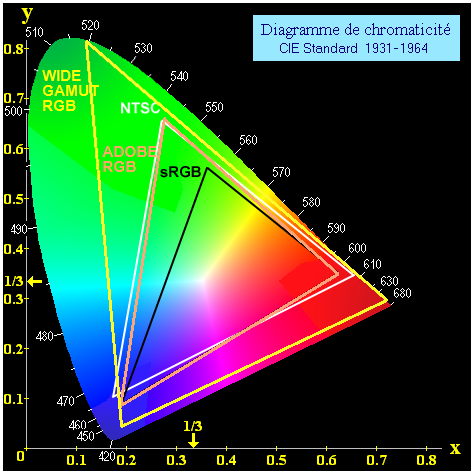
这里附上运行的 M代码(欢迎指点),以及若干常见换算矩阵:
- %% Run1.m %%
- clear
- idx= 0;
- for r= 0:20
- for g= 0:20
- for b= 0:20
- if(r+g+b>0)
- X = (-0.14282 * r) + (1.54924 * g) + (-0.95641 * b);
- Y = (-0.32466 * r) + (1.57837 * g) + (-0.73191 * b);
- Z = (-0.68202 * r) + (0.77073 * g) + (0.56332 * b);
- idx= idx+1;
- xc(idx) = (X) / (X + Y + Z);
- yc(idx) = (Y) / (X + Y + Z);
- end
- end
- end
- end
- plot(xc,yc, '.');
- axis equal
- axis([0 1 0 1]);
- %% Run2.m %%
- clear
- idx= 0;
- for r= 0:20
- for g= 0:20
- for b= 0:20
- if(r+g+b>0)
- X = (2.7688 * r) + (1.7517 * g) + (1.1301 * b);
- Y = (1.0000 * r) + (4.5906 * g) + (0.0601 * b);
- Z = (0 * r) + (0.0565 * g) + (5.5942 * b);
- idx= idx+1;
- xc(idx) = (X) / (X + Y + Z);
- yc(idx) = (Y) / (X + Y + Z);
- end
- end
- end
- end
- plot(xc,yc, '.');
- axis equal
- axis([0 1 0 1]);
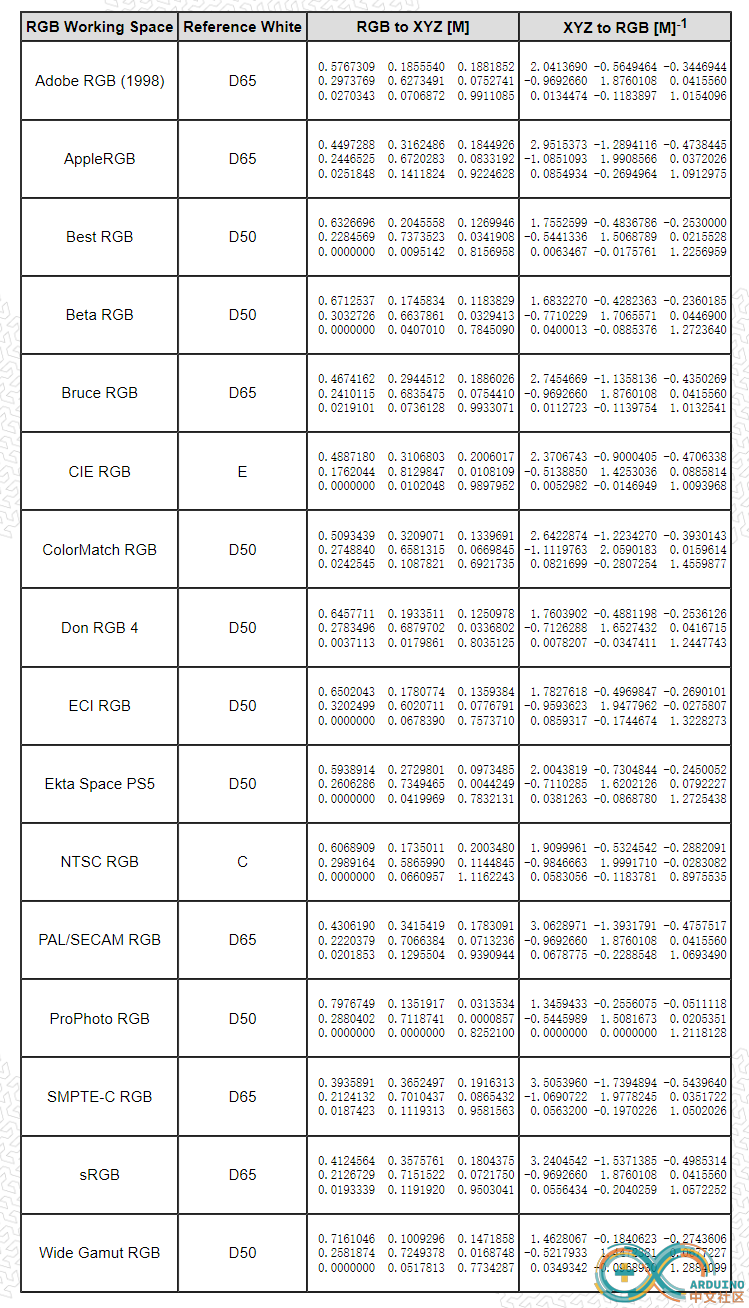
换算矩阵里的 CIE RGB 行就是和 Run2 一样效果,只是每个元素都等比例缩放了。
如果使用归一化坐标将和 Run2 结果一致。
【结论】
M5Stack 团队给大家科普了色度图的概念,这点的确不错。
但很不幸贴错了公式,导致 x,y 根本无法计算进马蹄区域。
正确的 RGB 转 XY 公式应该为(Run2算法,CIE-XYZ):
- X = (2.7688 * r) + (1.7517 * g) + (1.1301 * b);
- Y = (1.0000 * r) + (4.5906 * g) + (0.0601 * b);
- Z = (0 * r) + (0.0565 * g) + (5.5942 * b);
- xc = (X) / (X + Y + Z);
- yc = (Y) / (X + Y + Z);
或者按照上述表格中,选择一种合适的矩阵 M 作为 RGB 左乘因子:XYZ=[M] RGB
另外附上一片介绍颜色空间的文档:
 2010--kerr--cie_xyz.pdf
(237.04 KB, 下载次数: 8)
2010--kerr--cie_xyz.pdf
(237.04 KB, 下载次数: 8)
这篇文档就提及了颜色空间的选择不是惟一的(即M矩阵不唯一),
同时也提到了 Y 作为亮度出现在第二个维度的情况,但显然并不适用于马蹄图。
--------------------------------------------------------------------
以上,发现了 M5Stack 官方文档中的一点失误,以测评的形式记录之。
祝大家 DIY 愉快,万事如意!
|
|